Comment j’ai roulé avec Pythagore et Newton

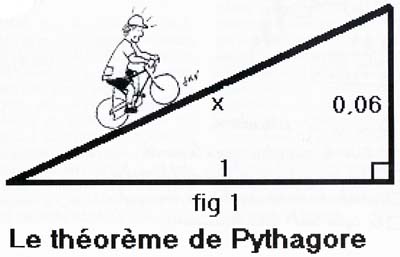
Si le cyclotouriste cherche son bonheur dans l’effort physique, la contemplation des paysages ou du patrimoine architectural plus que dans la compagnie des célébrités, il peut quand même lui arriver au cours de ses randonnées de se trouver en présence de véritables personnalités. Par exemple, mon ami Jean-Claude Berthommier, membre éminent de l’Orléans Cyclotouriste et du Club des Cent Cols, est un jour tombé (au sens figuré) sur Henri Bosc et son 650…

Mais peu d’entre nous peuvent se vanter d’avoir roulé avec des savants de renommée internationale, encore moins ceux que la rumeur publique donnait pour morts depuis respectivement 254 et 2481 ans. C’est pourtant ce qui m’est arrivé il y a un peu plus de vingt ans.

L’année 1981 avait été une année faste : elle avait vu, entre autres bonheurs, la naissance de mon premier fils, ma libération du service militaire et ma nomination comme professeur de mathématiques au lycée de Saint-Pol-sur-Ternoise (Pas-de-Calais). Après quelques mois passés vissé à mon bureau, j’ai commencé à éprouver comme une nostalgie de certains aspects de mon récent passé militaire ; pas tellement celle de l’adjudant, mais plutôt celle des petits footings quotidiens (Ah le canal de déviation de la Scarpe à 7 h du matin en novembre…).

A ma grande surprise j’avais découvert que, sans ressembler à l’Auvergne ni aux Vosges, le Pas de Calais est (un peu) vallonné et boisé, orné de charmants villages nichés au creux des vallées. L’idée avait fait son chemin petit à petit : j’allais me mettre au vélo.

C’est ainsi que, novice total, j’achetai mon premier vrai vélo (2 plateaux et 5 pignons, quel luxe !)… par correspondance. Après quelques sorties d’initiation, je me trouvais par un joli dimanche matin de mai 1982 à Auxi-le-Château sur le chemin du retour. C’est dans la côte qui commence sur la gauche, quand on laisse en face la route de Doullens et d’Arras, que j’ai compris que mon acquisition était dotée de développements mieux adaptés aux capacités d’un coureur qu’aux miennes… Je m’exhortais donc à devoir forcer un peu plus que prévu pour franchir les 60 m de dénivelé du kilomètre d’ascension, heureusement unique, que j’avais soigneusement mesuré sur une carte au 25000ème .

Sauf que… sauf que ce que j’avais mesuré, ce n’était pas – même au facteur d’échelle près – la vraie distance, mais sa projection sur la carte, qui est plus courte. A l’extrême, un alpiniste qui gravirait verticalement une paroi verrait son parcours sur la carte réduit à un seul point. Il allait donc me falloir grimper pendant un peu plus d’un kilomètre… oui mais de combien en plus ?

- « Facile mon gars, tu n’as qu’à utiliser mon théorème ! »

C’était le passager d’un lourd tandem qui montait encore plus lentement que moi qui venait de parler ; perdu dans mes pensées, je n’avais pas vu que je le rattrapais. Comment avait il su ce qui m’occupait ? Mystère !

Le personnage était surprenant : très bronzé, chauve comme un œuf avec une simple couronne de cheveux blancs et une énorme barbe frisée, vêtu d’un genre de drap et chaussé de simples sandales de cuir, il parlait avec un curieux accent chantant en roulant les R, sans que ses yeux noirs ne cessent de me sourire.

« Vois tu, ce que tu parcours en ce moment – avec quelque difficulté – ce n’est pas simplement une charmante petite route de campagne ; c’est aussi une hypoténuse, autrement dit le grand côté d’un colossal triangle rectangle, et dont tu veux trouver la longueur x. L’un des côtés de l’angle droit – celui que tu as répéré sur ta carte - mesure 1 km, l’autre 0,06 km. J’ai montré il y a bien longtemps la relation suivante, qui porte maintenant mon nom : x² = 1² + (0,06)² (voir fig 1) ; finalement x = \ 1,0036 km.

- Très astucieux monsieur…
- Pythagore, mon gars, Pythagore de Samos, à ton service ».
J’avais donc la formule mais pas la valeur numérique ; qui sait ce que peut valoir ?
- « Voyons my boy, avec mon invention tu peux avoir une valeur approchée »

J’étais arrivé au niveau du conducteur du tandem et, s’il avait comme son compagnon lu dans mes pensées, on n’aurait pu trouver plus différent. Il portait une vaste redingote avec des basques, des culottes et bas de soie et de petits escarpins vernis. Chauve ou pas, il arborait une gigantesque perruque qui moutonnait sur ses épaules et son dos ; aucune trace non plus de bonhomie méditerranéenne dans son regard clair et froid… que faisait donc ici cet austère Anglais (son accent ne pouvait pas tromper), à mi chemin entre Crécy et Azincourt ?

J’eus bien vite la réponse, il venait y faire des maths.

- « Ce dont tu as besoin, c’est à l’évidence d’ un développement limité.
- Je m’en aperçois bien, répondis-je quelque peu étourdiment, il me faudrait un plateau plus petit et un pignon plus grand. Mais comment les changer ici ? Je dois rentrer avec ces braquets.
- Il ne s’agit pas de cela ! tonna-t-il alors. Un développement limité, c’est une formule plus simple et qui donne presque la même valeur que ton x qui est en fin de compte du type \ 1+a avec a petit. En fait c’est très facile, à condition de prendre tout à l’envers.
- En descente, vous voulez dire ? Bien sûr que ce sera plus facile, mais ce n’est pas ma route.
- Silence ! Je n’ai jamais eu un étudiant aussi obtus que toi ! »

Je me gardai bien de lui révéler que, toutes proportions gardées, nous étions collègues, de peur d’accroître encore son mépris ; connaissant d’autre part la réputation des écoles anglaises en matière de châtiments corporels (encore en vigueur il n’y a pas si longtemps), je pris un peu de champ, en protégeant mes arrières et sans plus l’interrompre par des remarques irréfléchies.

- « Si tu fais d’abord le calcul pour le carré, tu verras que si b est petit, (1 + b)² est voisin de 1 + 2² ( il suffit de développer ).
Considéré à l’envers, tu trouves que \ 1+4 est voisin de 1 + a/2. Voilà ce que j’ai inventé : le calcul infinitésimal ! »
- C’est vous qui avez inventé… mais alors vous êtes…
- Well, Isaac Newton, from Cambridge, of course ».

En disant ces mots, ravi d’avoir enfin réussi à faire comprendre quelque chose à un si piètre auditeur, le vénérable universitaire se détendit un peu et me gratifia d’un sourire fugace.

C’est en atteignant le haut de la côte que j’achevai mes calculs : \ 1,0036 égale environ 1,0018 ; donc je venais de parcourir approximativement 1m80 de plus que le kilomètre prévu, en supposant bien sûr que la mesure sur la carte ait été correcte.

J’aurais bien aimé poursuivre ma discussion avec d’aussi éminents personnages mais, sourds à mes appels, ils disparurent presque instantanément, d’une accélération puissante qui me laissa sur place. Je n’ai aucun souvenir des 25 km qui suivirent pendant lesquels je restai plongé dans mes pensées. J’eus le temps de réaliser que le résultat de Pythagore demeurait exact si la route n’est pas droite, ce qui est bien le cas à Auxi et que, si a est assez petit, \ 1+a est toujours compris entre 1 + a/2 et 1 + a/2 - a²/8 ; donc que la distance approchée obtenue par Newton différait de la vraie de moins de 2 mm… Sur un peu plus d’un km… chapeau l’ancien !

Jusqu’ à ce jour je n’avais parlé de ma rencontre à personne, de peur de finir dans une camisole de force, mais je n’ai pas cessé de faire du vélo. Mon collègue et ami Daniel Petit m’a pris sous son aile et m’a initié au vrai cyclotourisme : matériel, fréquence de pédalage, braquets, entraînement , etc… Il m’a même permis d’essayer une de ses magnifiques randonneuses. J’ai depuis acquis moi aussi une de ces machines, véritable œuvre d’art du grand couturier orléanais André Thauvin. J’ai constaté qu’avec de la patience, un minimum d’entraînement et de courage et surtout des braquets adaptés, tout le monde peut aller ( presque ) n’importe où.

A mes amis qui me demandent pourquoi je m’acharne à escalader des côtes - certains rajouteraient volontiers à ton âge ou vu ton poids -, je fais les réponses habituelles : le plaisir de l’effort physique en liberté, la beauté des paysages et le moment de joie incomparable qu’on éprouve à l’arrivée au col. Mais la vraie raison n’est pas là… tout le monde sait bien que la terre n’est pas plate et même pas ronde, mais aplatie aux pôles.

Donc le calcul réalisé par mes deux compères n’est pas parfait. Voilà pourquoi je roule : je ne désespère pas de rencontrer un beau jour, dans une côte où je souffrirai les mille morts, un de ces géographes célèbres dont les noms apparaissent sur les cartes : Lambert, Clarke ou Mercator pour me détailler le vrai calcul… et pourquoi pas les trois ensemble ? Voilà pourquoi depuis vingt ans je roule, tout en gardant un œil sur les triplettes.

Jean-Marc Villermaux

CC n°5166